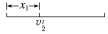# 匀变速直线运动的平均速度公式 [v−t 图像看位移]
# 平均速度公式
若一物体做匀加速直线运动,初速度为v0,末速度为v,位移为x,这段位移中间位置的瞬时速度为v2x。试用不同方法比较v2t 与v2x 的大小。
# 方法一 定性分析法
实际运动过程以匀加速直线运动为例,速度先慢后快,
前2t 时间内的位移x1<2x,故v2t<v2x
![]()
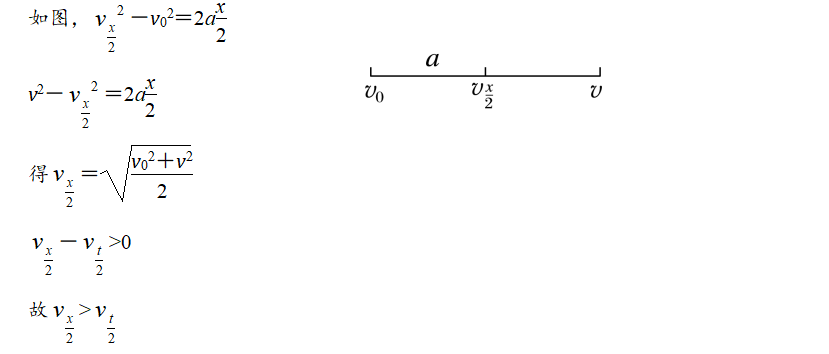
# 方法二 公式法
![]()
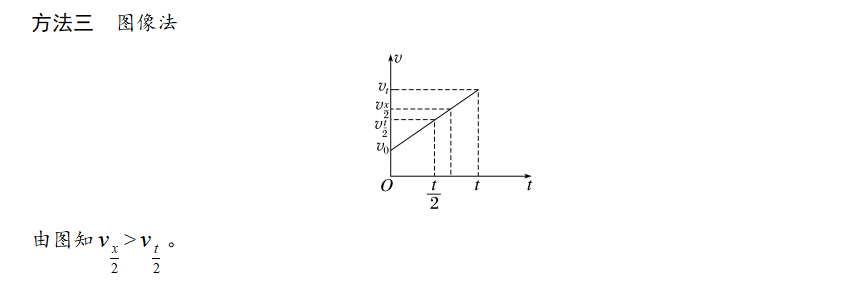
# 方法三 图像法
![]()
# 匀变速直线运动的位移与时间的关系
# 匀变速直线运动的位移
例 1 以 36km/h 的速度行驶的列车开始下坡,在下坡路上的加速度等于 0.2m/s2 ,经过 30s 到达坡底,求坡路的长度和列车到达坡底时的速度大小。
v=36km/h=10m/s, a=0.2m/s2, t=30s
v’=v+at=10m/s+0.2m/s2∗30s=16m/s
s=vt=(v+v’)∗t/2=26m/s∗30s/2=390m
例 2 一物体做匀减速直线运动,初速度大小为v0=5m/s,加速度大小为0.5m/s2 ,求:
(1) 物体在前3s 内的位移大小;
(2) 物体在第3s 内的位移大小。
(1) v=5m/s a=−0.5m/s2, t=3s
v’=v+at=5m/s−0.5m/s2∗3s=3.5m/s
s=vt=(v1+v2)∗t/2=8.5m/s∗3s/2=12.75m/s
(2) v1=4m/s, v2=3.5m/s, t=1s
s=vt=(v1+v2)∗t/2=7.5m/s∗1s/2=3.75m/s
# 速度与位移的关系
某型号航空母舰上装有帮助飞机起飞的弹射系统,已知某型号的飞机在平直跑道上加速时可产生的最大加速度为5.0m/s2,当飞机的速度达到50m/s 时才能离开航空母舰起飞,设航空母舰始终处于静止状态。问:
若某舰上不装弹射系统,要求该型号飞机仍能在此舰上正常起飞,该舰身长至少为多长?
v=50m/s a=5 m/s2
t=v/a=50ms−1/5ms−2=10s
s=vt/2==50m/s∗10s/2=250m
# 刹车中的位移问题
以18m/s 的速度行驶的汽车,制动后做匀减速直线运动,在3s 内前进36m (制动3s 时汽车未停止)。求汽车的加速度及制动后5s 内发生的位移大小。
(v−t∗a+v)∗t/2=s s=36m v=18m/s t=3s
∴a=−4m/s2
汽车在制动后5s 内的位移与4.5s 内的位移相等,此过程中可以看作反向的初速度为零
∴t2=4.5s s=(2v−at2)∗t2/2=40.5m
-
一质点做匀变速直线运动,其位移表达式为x=(10t+t2)m,则。
- 质点的初速度为10m/s
- 质点的加速度大小为1m/s2
- 质点的加速度大小为2m/s2
- 在第4s 末,质点距出发点24m
x=v0t+0.5at2
-
如图所示,高山滑雪运动员在斜坡上由静止开始匀加速滑行距离x1,又在水平面上匀减速滑行距离x2 后停下,测得x2=2x1,运动员经过两平面交接处速率不变,则运动员在斜坡上滑行的加速度a1 与在水平面上滑行的加速度a1 的大小关系为。
- a1=a2
- a1=4a2
- 2a1=a2
- a1=2a2
![]()
-
一小车从A 点由静止开始做匀加速直线运动,若到达B 点时速度为v,到达C 点时速度为2v,则xAB:xBC 等于。
- 1:1
- 1:2
- 1:3
- 1:4
![]()